X. 複素積分の定理公式を数値積分で確認（２）
5. Cauchyの積分定理の確認
Cauchyの積分定理というのは以下の通りです。
有界な単連結領域\(D\)で \(f(z)\) が解析的なら、\(D\)内のすべての単純閉曲線\(C\)に対して
積分記号に○が付いているのは閉曲線に沿った周回積分だからです。「有界な」というのは複素平面において有限の範囲に収まるという意味です。単連結領域\(D\)というのは、\(D\)内のすべての閉曲線が\(D\)内の点だけを囲むような領域、つまり穴が開いていない領域のことです。単純閉曲線というのは自分自身と交わらないループ状の曲線です。4節で確認した正則関数の積分値が経路によらないという結果は数学的にはCauchyの積分定理から証明されますが、Cauchyの積分定理についても複素数値積分で確認してみます。
\begin{equation}
\oint_C f(z) \, dz = 0 \tag{7} \label{g}
\end{equation}
となる。
下図はZIPでダウンロードできるcurve2num.xlsmのSheet2になりますが、今回用いる積分経路はこの閉曲線\(C\)です。「4.1 フリーハンド曲線の頂点の座標取得」で紹介したVBAマクロ「Sub 第1曲線頂点()」をそのまま使って頂点の座標を取得しています。ここでは、被積分関数
\begin{equation}
f(z) = \frac{1}{z} \tag{8} \label{e}
\end{equation}
に対してCauchyの積分定理を確認しますが、閉曲線\(C\)の内側に原点 \(0 + 0j\) を含まないというのがポイントになります。この閉曲線\(C\)は「6. Cauchyの積分公式の確認」でも、「7. 留数定理の確認」でも使いますが、前者で使う理由は \(-1 + 1j\) を含むから、後者は \(-2 + 0j\) と \(0 + 2j\) を含むからで、三者三様に異なります。
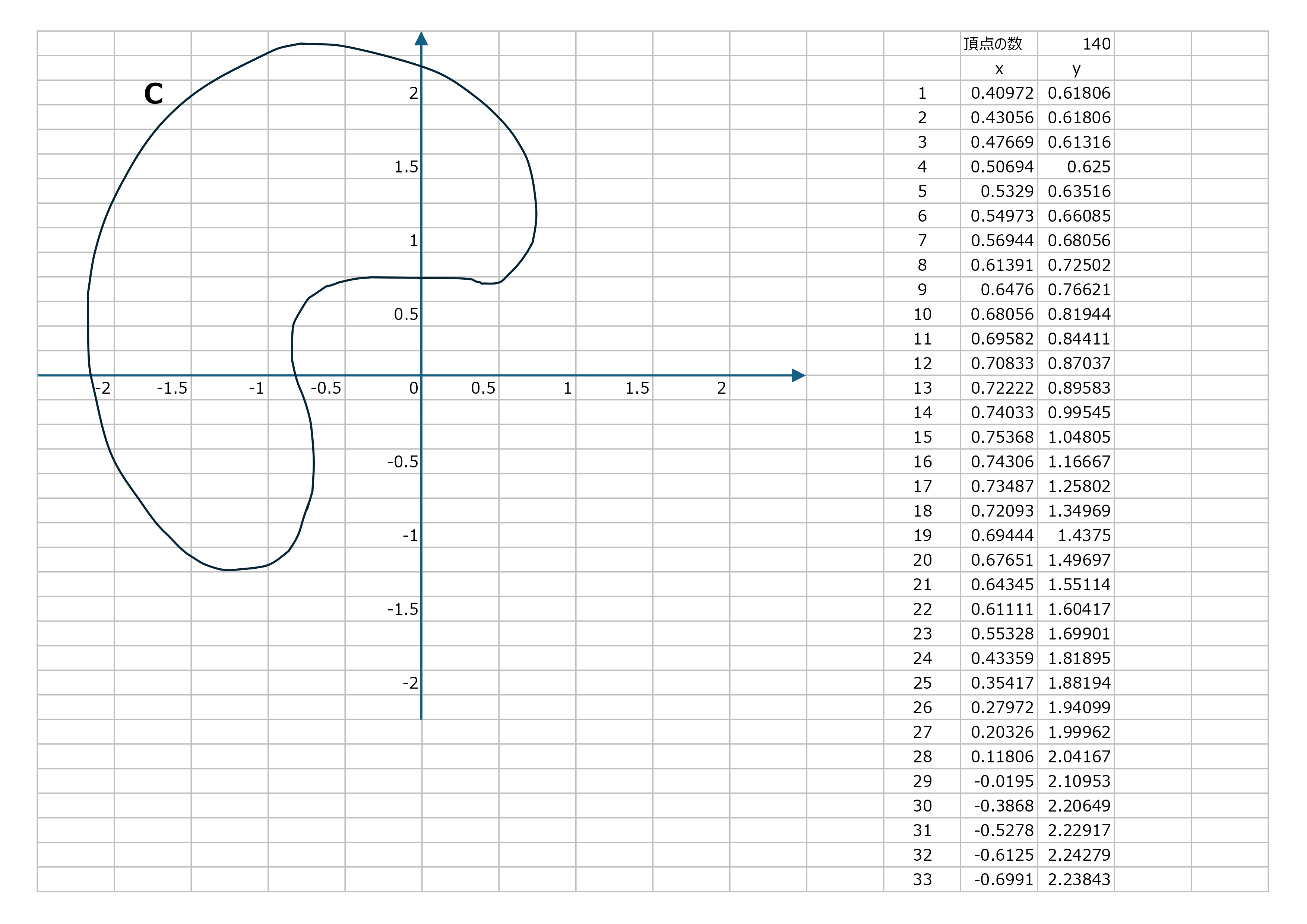画像を新しいタブで開くと高解像度で見ることができます。
式\eqref{e}の \(f(z)\) は原点においてのみ微分できません。従って、内側に原点を含まない閉曲線\(C\)に沿って積分すれば、結果は0になるはずです。この複素数値積分をするPythonプログラムは以下の通りです。基本的にはcplx_intgrl_2.pyと同じ構成ですが、積分経路が一つだけなので変数mに対するループはありません。それ以外の変更点は、4行目でsheet2を参照しており、21行目の被積分関数が式\eqref{e}になっていることです。26行目にある計算結果を見ると有効数字8～9桁で0 + 0jとなっており、Cauchyの積分定理通りになっています。
コードの表示にはPrism.jsを使用しています。prism.cssの設定は団塊爺ちゃんの備忘録を参考にしました。
import openpyxl
wb = openpyxl.load_workbook('(path to the xlsm file)/curve2num.xlsm')
sheet = wb['Sheet2']
i0 = 12
div = 1000
vertNum = sheet.cell(row=1, column=i0+2).value
vertArX = []
vertArY = []
for n in range(vertNum):
vertArX.append(sheet.cell(row=n+3, column=i0+1).value)
vertArY.append(sheet.cell(row=n+3, column=i0+2).value)
Sum = 0. + 0.j
for k in range(vertNum - 1):
z1 = complex(vertArX[k], vertArY[k])
z2 = complex(vertArX[k+1], vertArY[k+1])
for p in range(div):
z3 = z1 + (z2 - z1) * (0.5 + p) / div
Sum += (1 / z3) * (z2 - z1) / div
print(f"{Sum.real:.10f} + {Sum.imag:.10f}j")
# ----- Output -----
# -0.0000000096 + -0.0000000359j
6. Cauchyの積分公式の確認
Cauchyの積分公式というのは以下の通りです。
単連結領域\(D\)において解析的な関数 \(f(z)\) について
式\eqref{g}と式\eqref{f}の積分は何か紛らわしいですよね。両式とも \(f(z)\) は単連結領域\(D\)において解析的ですが、式\eqref{f}では被積分関数が \(f(z)\) を \((z - z_{0})\) で割ったものになっているのがミソです。\((z - z_{0})\) で割った関数全体は、\(z = z_{0}\) において微分不可能になります。そういう微分不可能な点が内側にある閉路で周回積分すると、その積分値は微分不可能な点\(z_{0}\)における \(f(z)\) の値 \(f(z_{0})\) の \(2\pi i\) 倍になるというのです。この摩訶不思議な公式の数学的な証明は別途教科書で学んでいただくとして、ここでは例によって複素数値積分による確認を行います。
\begin{equation}
f(z_{0}) = \frac{1}{2\pi i} \, \oint_C \frac{f(z)}{z - z_{0}} \, dz \tag{9} \label{f}
\end{equation}
となる。但し、\(z_{0}\)は\(D\)内の任意の点、\(C\)は\(z_{0}\)を取囲む\(D\)内の任意の単純閉曲線である。
積分経路には5節の閉曲線\(C\)を用いるので、その内側にある点を選んで \(z_{0} = -1 + 1j\) とします。\(f(z)\) には3節と4節で用いた式\eqref{h}を用いますが、ここに再掲します。
\begin{equation}
f(z) = z^{2} + 3z + 1 \tag{3} \label{h}
\end{equation}
このお膳立てで式\eqref{f}右辺にある複素数値積分を行いますが、左辺に \(2\pi i\) を移項した \(2\pi i\,f(z_{0})\) についても別途数値計算して積分値と比較します。以下がそのプログラムです。24行目までの積分プログラムは今までに出てきたものと同じですが、23行目の被積分関数は式\eqref{h}を \((z - z_{0})\) で割ったものになっています。一方、27行目は \(2\pi i\,f(z_{0})\) を数式通りに計算しているだけです。両者の計算結果を比較すると、有効数字8～9桁で一致しているのが分ります。
import openpyxl
import math
wb = openpyxl.load_workbook('(path to the xlsm file)/curve2num.xlsm')
sheet = wb['Sheet2']
i0 = 12
div = 1000
vertNum = sheet.cell(row=1, column=i0+2).value
vertArX = []
vertArY = []
for n in range(vertNum):
vertArX.append(sheet.cell(row=n+3, column=i0+1).value)
vertArY.append(sheet.cell(row=n+3, column=i0+2).value)
Sum = 0. + 0.j
z0 = complex(-1., 1.)
for k in range(vertNum - 1):
z1 = complex(vertArX[k], vertArY[k])
z2 = complex(vertArX[k+1], vertArY[k+1])
for p in range(div):
z3 = z1 + (z2 - z1) * (0.5 + p) / div
Sum += (pow(z3, 2) + 3 * z3 + 1) / (z3 - z0) * (z2 - z1) / div
print(f"Integral: {Sum.real:.10f} + {Sum.imag:.10f}j")
# Calculation for 2πj∙f(z0)
dpj_fz0 = complex(0., 2. * math.pi) * (pow(z0, 2) + 3 * z0 + 1)
print(f"2πj∙f(z0): {dpj_fz0.real:.10f} + {dpj_fz0.imag:.10f}j")
# ----- Output -----
# Integral: -6.2831852832 + -12.5663706052j
# 2πj∙f(z0): -6.2831853072 + -12.5663706144j
Cauchyの積分公式から導かれるGoursatの定理についても数値積分で確認します。Goursatの定理は以下の通りです。\(n = 0\) の時がCauchyの積分公式です（拡張された階乗の定義で \(0 \, ! = 1\)）。
単連結領域\(D\)において解析的な関数 \(f(z)\) について、\(D\)内の点 \(z = z_{0}\) における\(n\)階微分の値 \(f^{(n)}(z_{0})\) は
\begin{equation}
f^{(n)}(z_{0}) = \frac{n \, !}{2\pi i} \, \oint_C \frac{f(z)}{(z - z_{0})^{n+1}} \, dz \qquad (n = 0, 1, 2,...) \tag{10}
\end{equation}
となる。
確認は1階微分などとケチ臭いことを言わず、2階微分にしてみます。
\begin{equation}
f^{(2)}(z_{0}) = \frac{1}{\pi i} \, \oint_C \frac{f(z)}{(z - z_{0})^{3}} \, dz \tag{11} \label{i}
\end{equation}
となるわけですが、積分経路には5節の閉曲線\(C\)を用い、 \(z_{0} = -1 + 1j\) とします。\(f(z)\) には式\eqref{h}を用いることにすると、2階導関数は簡単に求められて
\begin{equation}
f^{(2)}(z) = 2 \tag{12}
\end{equation}
です。従って、式\eqref{i}右辺の積分値は \(2\pi i\) となるはずです。以下のプログラムで数値積分すると有効数字7桁で一致していますが、精度は若干悪くなるようです。
import openpyxl
import math
wb = openpyxl.load_workbook('(path to the xlsm file)/curve2num.xlsm')
sheet = wb['Sheet2']
i0 = 12
div = 1000
vertNum = sheet.cell(row=1, column=i0+2).value
vertArX = []
vertArY = []
for n in range(vertNum):
vertArX.append(sheet.cell(row=n+3, column=i0+1).value)
vertArY.append(sheet.cell(row=n+3, column=i0+2).value)
Sum = 0. + 0.j
z0 = complex(-1., 1.)
for k in range(vertNum - 1):
z1 = complex(vertArX[k], vertArY[k])
z2 = complex(vertArX[k+1], vertArY[k+1])
for p in range(div):
z3 = z1 + (z2 - z1) * (0.5 + p) / div
Sum += (pow(z3, 2) + 3 * z3 + 1) / pow((z3 - z0), 3) \
* (z2 - z1) / div
print(f"Integral: {Sum.real:.10f} + {Sum.imag:.10f}j")
# Calculation for 2πj
dpj = complex(0., 2. * math.pi)
print(f"2πj : {dpj.real:.10f} + {dpj.imag:.10f}j")
# ----- Output -----
# Integral: 0.0000001012 + 6.2831854978j
# 2πj : 0.0000000000 + 6.2831853072j
7. 留数定理の確認
（以下、現在作成中・・・）