駄待ち狐：複素積分(1)

X. 複素積分の定理公式を数値積分で確認（１）

1. 「雌伏の至福」を今ひとたび

IV章の最後に「Google Search Consoleによれば、過去6ヶ月間にグーグル検索で本サイトが表示された回数は217回で、クリックされた回数は22回だそうです」と書きましたが、2016年1月15日現在も過去3ヶ月間にグーグル検索で本サイトが表示された回数は397回で、クリックされた回数は12回と低迷しています。タイトル画像に記載しているfoxのアドレス宛てのメールは一通も届いていません。このままでは「お便りありがとう」というX章を書き起こせる日が来るとは思えないので、別の内容でX章を書くことにします。

III章の最後に

共振器のモード解析という視点で見ると、40年間に亘る手持ち（頭持ち？）ネタだったことになります。「？？？」の気色悪さが年月を経て「！！！」になることは、駄待ち狐にとって無上の喜びです。それに要した年月が長いほどその満足感は大きくなります。・・・雌伏のままでも至福はあるということです。

と書いています。そういう「雌伏の至福」をまた味わおうとここ1ヶ月ほどの間取組んできたのが複素積分です。複素積分は複素関数（複素数上で定義された関数）の積分で、高校レベルの数学には登場せず、大学で学ぶ数学になります。

駄待ち狐は教養課程で微積分学を履修しましたが、残念ながら複素積分にまでは話が及びませんでした。前期の大半が「実数とは何か？」といった哲学的な話題に終始したためです。一方、専門課程（電気電子工学）に入ると、複素積分の話題は度々出てくるのですが、数学的証明はすっ飛ばして数学で得られる結果だけを工学のために利用するという立場です。「複素平面上の閉路に沿った積分は閉路内に含まれる留数の和になる」という留数定理も何回か出てくるのですが、そこに至る話はないので「そりゃシンプルでいいですけど、何でですか？」状態です。留数とはそもそも何なのかもよく分かりません。

そこで改めて複素積分の勉強をしようと思い立った訳ですが、今回は教科書は買わずググった中で一番よさそうな複素関数論（講義ノート）を勉強しました。その結果、留数定理の証明に至るまでが腑に落ちました。因みに、同書の「6.3　解析関数の微分の公式」の証明については疑問があったのでコーシーの積分公式【証明と例題】の中のグルサの定理（解析関数の微分の公式と同じもの）の証明を参照しました。また、「9.2　ローラン級数」には導出の概略しか書かれていなかったので、ローラン展開の意味・計算方法・特異点の分類を読んで勉強しました。これで、大学の専門課程以来47年間続いてきた「？？？」が「！！！」になりました。

2. そこで何をプログラミングしたのか・・・

このサイトはプログラムを紹介するのが本旨ですが、何をプログラミングしたのかを説明するために複素関数の微分と積分について最小限の説明をします。詳細については上記の引用サイトをご熟読下さい。複素数とは何かについては高校の数学でも出てくるので割愛しますが、複素関数 \(w = f(z)\) は各複素数\(z\)に対してある複素数\(w\)を対応させる規則（写像）です。実関数（実数上で定義された関数） \(y = f(x)\) の場合と同様に

\begin{equation} \frac{d \, f(z_{0})}{dz} \equiv \lim_{\Delta z\to0} \frac{f(z_{0} + \Delta z) - f(z_{0})}{\Delta z} \label{b} \end{equation}

が存在するとき、\(f(z)\) は \(z = z_{0}\) で微分可能であると言います。（数式を美しく表記できているのはMathJaxのおかげです。MathJaxの使い方に分かりやすい解説があります。）

複素関数の微分では、\(\Delta z\)を複素平面上でどの方向からゼロに近づけても同じ値に収束することが必要になります。複素関数の微分可能性は実関数の微分可能性に比べて非常に厳しい制約となっているため、逆にある点で1回微分できる複素関数はその点で何回でも微分できるという性質があります。ある領域（定義域）で微分可能な関数のことを正則関数と呼びます。正則関数はべき級数（Taylor級数）で表現できる（解析的である）ので、正則関数のことを解析関数とも言います。何か禅問答めいてきましたが、さらに複素積分に進みます。

複素関数の微分の時の「複素平面上でどの方向からゼロに近づけても」という条件に呼応して、複素積分では複素平面上のどの経路に沿って積分するのかが問題になります。複素平面上の経路\(C\)を\(n\)個の区間に分割してその分割点（経路上\(C\)の点）を順番に \(z_{0}, z_{1}, \dots z_{n}\) とします。\(z_{0}\)は始点、\(z_{n}\)は終点です。これを用いて、複素関数 \(f(z)\) の経路\(C\)に沿った線積分を

\begin{equation} \int_C f(z) \, dz \equiv \lim_{n\to\infty} \sum_{i=1}^{n} f(\hat{z}_{i}) \, \Delta z_{i} \qquad (\Delta z_{i} \equiv z_{i} - z_{i-1}) \label{a} \end{equation}

と定義します。ただし、複素平面上での区間の幅 \(|\Delta z_{i}|\) は分割数\(n\)を大きくするにつれてゼロに近づくものとします。和を取る時に用いる関数値 \(f(\hat{z}_{i})\) は、経路\(C\)上で\(i\)番目の区間内にある任意の点\(\hat{z}_{i}\)（\(z_{i-1}, \hat{z}_{i}, z_{i}\) がこの順番に並んでいる）における値です。

複素積分では複素平面上のどの経路に沿って積分するのかが問題になると書きましたが、正則関数をその定義域内の経路に沿って積分する場合は、始点・終点が同じ複数の経路に対する積分値は同じになります。これは数学的にはCauchyの積分定理から導き出されるのですが、直感的には納得しにくい話です。式\eqref{a}に出てくる \(f(\hat{z}_{i})\) も \(|\Delta z_{i}|\) も複素数なので、実際に数値計算をするとなると非常に面倒な話です。こんな面倒な計算を複数の経路に対して行って、本当に同じ値になるのでしょうか？もちろん、そうなることが数学的に証明されているので間違いのない話なのですが、それは数学者的な思考です。

「理屈はそうだけど、その通りにはいかないよね」というのが現実世界で、その現実世界でモノづくりをするのが技術者です。駄待ち狐は技術者なので、本当にそうなるかどうかを確かめたいと思いました。式\eqref{a}を手計算するというのは途方もない話ですが、複素数を自在に操るPythonという強い味方がいます。この複素数値積分をPythonプログラムでやってみるというのが本章の狙いです。さらに言うと、式\eqref{b}の「\(f(z)\) が正則関数なら\(\Delta z\)を複素平面上でどの方向からゼロに近づけても同じ値になる」というのも納得しにくい話です。右辺の分母も分子も複素数なのに、本当に同じ値になるのでしょうか？次節ではまずこのことから確かめてみます。

3. 正則関数の微分が同じ値になることの確認

前置きが長くなりましたが、式\eqref{b}で\(\Delta z\)を複素平面上でどの方向からゼロに近づけても同じ値になることを確認するプログラムを紹介します。このプログラムでは

\begin{equation} f(z) = z^{2} + 3z + 1 \label{c} \end{equation}

とし、\(z_{0} = 2.3 + 1.7j\) における微分を計算しています。Pythonでは虚数単位として \(i\) ではなく \(j\) を用いますが、これは電気工学の慣習に従っているためです。電気・電子工学の分野では、電流を表す記号に \(i\) または \(I\) を使用します。そのため、虚数単位にも \(i\) を使うと、数式中でどちらを指しているのか区別できなくなるために、\(i\) の次にある \(j\) を虚数単位として用います。Pythonを愛する電気工学博士の駄待ち狐にとって、こんな嬉しい話はありません。

コードの表示にはPrism.jsを使用しています。
prism.cssの設定は団塊爺ちゃんの備忘録を参考にしました。


import random

z0 = 2.3 + 1.7j
abs_dz = 1. / 1e3

for n in range(5):
    dz = complex(random.uniform(-1, 1), random.uniform(-1, 1))
    if abs(dz) != 0.:
        dz *= abs_dz / abs(dz)
        dfdz = ((pow(z0 + dz, 2) + 3 * (z0 + dz) + 1)
               - (pow(z0, 2) + 3 * z0 + 1)) / dz
        print(f"dz = {dz.real:.5e} + {dz.imag:.5e}j")
        print(f"df/dz = {dfdz.real:.5f} + {dfdz.imag:.5f}j")


# ----- Output (Example by Chance) -----
# dz = -9.99987e-04 + -5.09856e-06j
# df/dz = 7.59900 + 3.39999j
# dz = 2.75119e-04 + -9.61410e-04j
# df/dz = 7.60028 + 3.39904j
# dz = -3.22004e-04 + 9.46738e-04j
# df/dz = 7.59968 + 3.40095j
# dz = 5.74991e-04 + 8.18160e-04j
# df/dz = 7.60057 + 3.40082j
# dz = 6.27899e-04 + -7.78295e-04j
# df/dz = 7.60063 + 3.39922j

プログラムの説明ですが、「複素平面上でどの方向から」を実証するために、7行目でdz（プログラム上は\(\Delta z\)をdzと表記）の実部と虚部を乱数で設定しています。random.uniform(-1, 1)で-1から1の範囲の乱数が生成されるので、9行目でdzの絶対値abs(dz)がabs_dzとなるように乗算することで「ゼロに近づけ」ます。abs_dzは4行目で設定しており、ここでは1/1,000としています。10～11行目で式\eqref{b}をそのまま計算していますが、Pythonで複素数に対してz^2とやると"TypeError: unsupported operand type(s) for ^: 'complex' and 'complex'"と叱られるので、組込み関数であるpow(z, 2)を使います。

本プログラムでは5回同じ計算を繰返していますが、dzを乱数で指定しているので毎回結果は異なります。プログラムを再度走らせると、また違った結果になります。因みに8行目のif文は実部と虚部が共に0になった場合（天文学的に低い確率ですが）にエラーとなるのを防ぐものです。毎回違う結果とはいえ、df/dzは有効数字3桁で7.6 + 3.4jになっています。式\eqref{c}の導関数が

\begin{equation} \frac{d \, f(z)}{dz} = 2z + 3 \end{equation}

であることを考えると、納得がいく結果です。上記プログラムでabs_dz = 1. / 1e7にして、df/dzの表示桁数も増やすと以下のような出力になり、「どの方向からゼロに近づけても同じ値に収束すること」が確認できます。


import random

z0 = 2.3 + 1.7j
abs_dz = 1. / 1e7

for n in range(5):
    dz = complex(random.uniform(-1, 1), random.uniform(-1, 1))
    if abs(dz) != 0.:
        dz *= abs_dz / abs(dz)
        dfdz = ((pow(z0 + dz, 2) + 3 * (z0 + dz) + 1)
               - (pow(z0, 2) + 3 * z0 + 1)) / dz
        print(f"dz = {dz.real:.5e} + {dz.imag:.5e}j")
        print(f"df/dz = {dfdz.real:.10f} + {dfdz.imag:.10f}j")


# ----- Output (Example by Chance) -----
# dz = 6.86584e-08 + -7.27051e-08j
# df/dz = 7.6000000511 + 3.3999999377j
# dz = 9.31459e-08 + 3.63846e-08j
# df/dz = 7.6000001059 + 3.4000000461j
# dz = -1.89274e-08 + 9.81924e-08j
# df/dz = 7.6000000051 + 3.4000001014j
# dz = 7.66391e-08 + 6.42374e-08j
# df/dz = 7.6000000763 + 3.4000000650j
# dz = -9.16472e-08 + 4.00099e-08j
# df/dz = 7.5999999052 + 3.4000000378j

4. 正則関数の積分値が経路によらないことの確認

4.1 フリーハンド曲線の頂点の座標取得（VBA）

式\eqref{a}を数値計算しようとした時に問題になるのは、複素平面上の経路\(C\)をどうやってプログラムに取込むかです。教科書ではフリーハンド曲線で経路の概念図（例えば「複素関数論」の図8）が示されますが、その後に実際に計算する段になると数式で経路を指定しています。「どんな経路に対しても」ということを確かめるには、やはり概念図通りのフリーハンド曲線に沿った積分をしてみたいものです。さて、手書きした曲線をなるべく労力をかけずに数値化するにはどうしたらいいか・・・と考えを巡らすと、思い当たるのはPowerPointやExcelにあるフリーフォーム図形の入力機能です。

フリーフォーム図形の入力はメニューを挿入→図形→線と辿るとその最後にあり、マウスをクリックしながら移動させるとその通りの曲線が表示されます。描かれた図形は「頂点の編集」ができることから、頂点（屈曲点）の座標が数値化されているのが分ります。この頂点座標をPythonのリストにする方法ですが、ExcelでVBAマクロを使うと頂点の(x, y)座標を全てシート上のセルに書出すことができます。次に、III章の「6. Pythonプログラム」に出てくるopenpyxlモジュールを使えば、Pythonに(x, y)座標を取込むことができます。xを実部、yを虚部とする複素数が複素平面上の曲線の頂点 \(z_{0}, z_{1}, \dots z_{n}\) になります。

VBAマクロを仕込んだExcelファイルはZIPでダウンロードできるようにしていますが、Sheet1は下図のようになっています。左側には複素平面の座標軸が示され、フリーハンド曲線\(C_{1}\)と\(C_{2}\)が描かれています。\(C_{1}\)も\(C_{2}\)も始点は\(z_{0}\)で終点は\(z_{n}\)です。右側には数値が並んでいますが、\(C_{1}\)と\(C_{2}\)の頂点の座標になります。一番上には頂点の数が示されていますが、\(C_{1}\)と\(C_{2}\)では頂点の数が異なります。これはExcel自身のアルゴリズムで曲線を近似するのに最適な頂点数が選ばれているものと考えられます。頂点の座標は複素平面の座標軸に付した目盛りに対応しています。

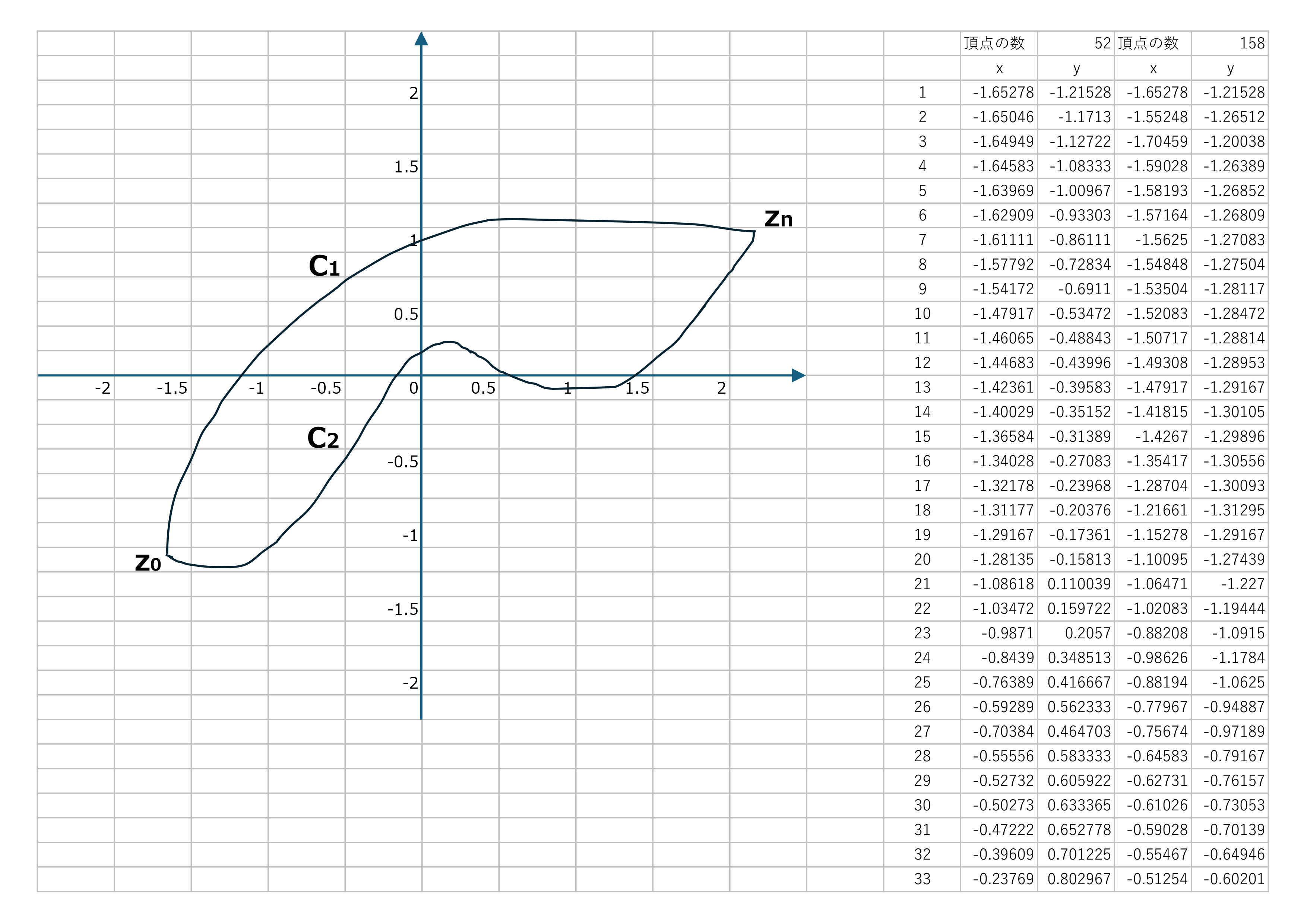画像を新しいタブで開くと高解像度で見ることができます。

頂点の座標を取得するマクロは以下の通りです。2行目でShapes(3)の頂点の座標がvertArrayに代入されます。座標軸の矢印がShapes(1)とShapes(2)なので、最初に描いた曲線がShapes(3)です。曲線を全て削除して新たに描くと、やはりShapes(3)になります。vertArrayは2次元配列になっていて、vertArray(n, 1)がn番目のx座標、vertArray(n, 2)がy座標です。5～7行目で前のデータを削除し、10行目では3行目で取得したvertArrayの最大要素番号を頂点の数としてCells(1, i0 + 2)に入力しています。i0は数値入力を右側にずらすためのオフセットです。15～19行目のForループで座標の値をセルに入力しますが、17～18行目で座標変換をしています。


Sub 第1曲線頂点()
  vertArray = ActiveSheet.Shapes(3).Vertices
  vertNum = UBound(vertArray)
  i0 = 12
  For m = i0 To i0 + 4
    Columns(m).ClearContents
  Next m

  Cells(1, i0 + 1).Value = "頂点の数"
  Cells(1, i0 + 2).Value = vertNum
  Cells(2, i0 + 1).Value = "x"
  Cells(2, i0 + 2).Value = "y"
  Rows(2).HorizontalAlignment = xlCenter
  Columns(i0).HorizontalAlignment = xlCenter
  For k = 1 To UBound(vertArray)
    Cells(k + 2, i0).Value = k
    Cells(k + 2, i0 + 1).Value = (vertArray(k, 1) - 270) / 108
    Cells(k + 2, i0 + 2).Value = (252 - vertArray(k, 2)) / 108
  Next k

End Sub

Sub 第2曲線頂点()
  vertArray = ActiveSheet.Shapes(4).Vertices
  vertNum = UBound(vertArray)
  i0 = 12
  For m = i0 + 3 To i0 + 4
    Columns(m).ClearContents
  Next m

  Cells(1, i0 + 3).Value = "頂点の数"
  Cells(1, i0 + 4).Value = vertNum
  Cells(2, i0 + 3).Value = "x"
  Cells(2, i0 + 4).Value = "y"
  Rows(2).HorizontalAlignment = xlCenter
  For k = 1 To UBound(vertArray)
    Cells(k + 2, i0 + 3).Value = (vertArray(k, 1) - 270) / 108
    Cells(k + 2, i0 + 4).Value = (252 - vertArray(k, 2)) / 108
  Next k

End Sub

Excel自身の座標はシートの左上隅が原点で、x軸は右向きが正、y軸は下向きが正です。数値の単位はポイント（pt）になっています（1 pt = 1/72 in = 0.35 mm）。これでは分りにくいので、シート上に描いたy軸に合うようにy座標を反転し、x軸とy軸の目盛りに合せて原点とスケールを変更しています。この時の変換パラメータは、セルサイズが54 pt × 18 ptであることから算出可能です。23行目以降は、第1曲線Shapes(3)と同様のやり方で第2曲線Shapes(4)の頂点座標を取得するマクロです。2つのマクロを実行した後、\(C_{1}\)と\(C_{2}\)で始点\(z_{0}\)と終点\(z_{n}\)が完全に一致するように、自動入力された値をそこだけ修正します。

4.2 取得した座標に沿った数値積分（Python）

いよいよPythonによる複素数値積分です。被積分関数には式\eqref{c}を使うことにして、以下のプログラムを作成しました。3～4行目はopenpyxlでcurve2num.xlsmのSheet1からセルの値を取得するための準備です。7行目からの変数mに対するforループで、\(C_{1}\)と\(C_{2}\)に対する計算を繰返します。10行目で頂点の数vertNumを取得し、14～15行目で頂点のx座標リストvertArXと、y座標リストvertArYを取得します。18～22行目のforループで式\eqref{a}の \(\Sigma\) を計算しますが、各ループで分割区間ごとの計算をした結果をSumに加算していきます。各区間の両端の座標を複素数z1、z2に変換して、\(\hat{z}_{i}\) に相当するz3はz1とz2の中点としています。


import openpyxl

wb = openpyxl.load_workbook('(path to the xlsm file)/curve2num.xlsm')
sheet = wb['Sheet1']
i0 = 12

for m in range(2):
    col_m1 = i0 + m * 2 + 1
    col_m2 = i0 + m * 2 + 2
    vertNum = sheet.cell(row=1, column=col_m2).value
    vertArX = []
    vertArY = []
    for n in range(vertNum):
        vertArX.append(sheet.cell(row=n+3, column=col_m1).value)
        vertArY.append(sheet.cell(row=n+3, column=col_m2).value)

    Sum = 0. + 0.j
    for k in range(vertNum - 1):
        z1 = complex(vertArX[k], vertArY[k])
        z2 = complex(vertArX[k+1], vertArY[k+1])
        z3 = (z1 + z2) / 2
        Sum += (pow(z3, 2) + 3 * z3 + 1) * (z2 - z1)
    print(f"C{m + 1}:  {Sum.real:.5f} + {Sum.imag:.5f}j")


# ----- Output -----
# C1:  8.03517 + 9.50693j
# C2:  8.04518 + 9.50977j

\(C_{1}\)に対する計算結果と\(C_{2}\)に対する計算結果は、有効数字3～4桁目から食違っており、まあ大体合ってるけど、精度的には物足りないなあといった感じです。分割数をもっと増やしたいところですが、頂点の数はExcelが決めているので増やせません。そこで考えたのが、頂点間の線形補間で区間の幅を小さくすることです。このプログラムを以下に示します。上記のプログラムとの違いは22～24行目で、6行目で設定した分割数div = 1000で頂点間をさらに細かく区切ります。区間の幅は24行目に出てくる(z2 - z1) / divになり、p番目の区間のz3は23行目のようになります。これで有効数字8～9桁目まで計算結果が一致するようになりました。


import openpyxl

wb = openpyxl.load_workbook('(path to the xlsm file)/curve2num.xlsm')
sheet = wb['Sheet1']
i0 = 12
div = 1000

for m in range(2):
    col_m1 = i0 + m * 2 + 1
    col_m2 = i0 + m * 2 + 2
    vertNum = sheet.cell(row=1, column=col_m2).value
    vertArX = []
    vertArY = []
    for n in range(vertNum):
        vertArX.append(sheet.cell(row=n+3, column=col_m1).value)
        vertArY.append(sheet.cell(row=n+3, column=col_m2).value)

    Sum = 0. + 0.j
    for k in range(vertNum - 1):
        z1 = complex(vertArX[k], vertArY[k])
        z2 = complex(vertArX[k+1], vertArY[k+1])
        for p in range(div):
            z3 = z1 + (z2 - z1) * (0.5 + p) / div
            Sum += (pow(z3, 2) + 3 * z3 + 1) * (z2 - z1) / div
    print(f"C{m + 1}:  {Sum.real:.10f} + {Sum.imag:.10f}j")


# ----- Output -----
# C1:  8.0458494029 + 9.5099356132j
# C2:  8.0458494129 + 9.5099356160j

4.3 不定積分による答合せ（Python）

経路\(C_{1}\)に沿って積分しても経路\(C_{2}\)に沿って積分しても結果が同じになることは確認できましたが、そもそもこの値は正しいのでしょうか。式\eqref{c}に対しては不定積分を求めることができるので、不定積分からも積分値を求めてみます。実関数の場合と同様に

\begin{equation} \int (z^{2} + 3z + 1) \, dz = \frac{1}{3}z^{3} + \frac{3}{2}z^{2} + z + C \end{equation}

（ここでの\(C\)は積分定数）なので、次式でも\(z_{0}\)から\(z_{n}\)までの積分値を計算できます。

\begin{equation} \int_{z_{0}}^{z_{n}} (z^{2} + 3z + 1) \, dz = \left[ \, \frac{1}{3}z^{3} + \frac{3}{2}z^{2} + z \, \right]_{z_{0}}^{z_{n}} \label{d} \end{equation}

\(z_{0}\)と\(z_{n}\)は手書き曲線の端点なので小数点以下が長々と続き、式\eqref{d}の右辺を手計算するのは面倒な話です。ここもPythonに頼り、以下のプログラムで計算します。


import openpyxl

wb = openpyxl.load_workbook('(path to the xlsm file)/curve2num.xlsm')
sheet = wb['Sheet1']
i0 = 12

vertNum = sheet.cell(row=1, column=i0+2).value
vertArX = []
vertArY = []
vertArX.append(sheet.cell(row=3, column=i0+1).value)
vertArX.append(sheet.cell(row=vertNum+2, column=i0+1).value)
vertArY.append(sheet.cell(row=3, column=i0+2).value)
vertArY.append(sheet.cell(row=vertNum+2, column=i0+2).value)
z0 = complex(vertArX[0], vertArY[0])
zn = complex(vertArX[1], vertArY[1])

valIndInt = []
for z in [z0, zn]:
    valIndInt.append((1 / 3) * pow(z, 3) + (3/2) * pow(z, 2) + z)
difIndInt = valIndInt[1] - valIndInt[0]
print(f"{difIndInt.real:.10f} + {difIndInt.imag:.10f}j")


# ----- Output -----
# 8.0458494136 + 9.5099356162j

前2つのプログラムと同様にcurve2num.xlsmのSheet1から経路\(C_{1}\)のx座標vertArXとy座標vertArYを取得しますが、本プログラムでは始点と終点の座標のみを読出しています（10～13行目）。この座標を14～15行目でz0とznに変換します。18～19行目でz0とznに対する式\eqref{d}の右辺の[]内を計算し、20行目でその差を求めています。得られた結果はコツコツと経路に沿って積分した値と有効数字8桁で一致しています。全く異なるアプローチで同じ結果が得られるというのは、「検算」の王道です。以上の結果は数学的に証明された当り前のことですが、複素数値積分のプログラムが正しく動作することが確認できたとも言えるでしょう。

更新日: 2026年1月31日