IX. 深層強化学習をROS/AnyLogicに導入（１）
1. プログラム作成の背景
「VII. ROSによるAMRのシミュレーション」のエピローグで述べた通り、ROSをいじり出した当初から深層学習/深層強化学習をROSに取込むという目論見があり、AnyLogicでも同様の思いがありました。深層学習（deep learning: DL）というのは人間の脳の神経回路を模したニューラルネットワーク（NN）を用いた機械学習の手法で、NNを多層化したDNN（deep neural network）を使うので"deep"が冠せられています。深層学習で最も有名なのは、同じもの（猫の顔、道路標識、バッグ等々）の色々な画像を大量に学習させることで、新規の画像が何であるかを判定する画像認識技術です。2013～2018年頃には「これぞまさしくAIだ」と喧伝されました。
因みに「これぞAI」は時代とともに変遷しています。1946年に世界最初のコンピュータENIACが登場した10年後の1956年には既に人工知能（artificial intelligence）という言葉が生れており、1950～60年代には探索・推論アルゴリズム（どんな問題でも解ける?!）がAIと呼ばれました。1980年代にはエキスパートシステム（医者の代りに診断ができる）、1990年代には単層のNN（巡回セールスマン問題が解ける）とファジー理論（「手の平で棒立て」ができる）、2010年代には深層学習（猫の顔が分る）がAIだとされました。2020年代は量子コンピュータ（素因数分解ができる）かと思っていたら、生成AIが一世を風靡することになりました。
AIでできることがだんだん小粒になっているような気がしますが、実は探索・推論アルゴリズムで解けたのは「ハノイの塔」（説明しないのでグーグって下さい）だけだし、エキスパートシステムで診断できたのは特異な疾患一つだけです。この「何か一つできたから全てができる」という大言壮語はAI学者の十八番です。ただ、一つのことができただけでも画期的だと思うのはグーグル（DeepMind社）のAlphaGoです。チェスよりも将棋よりも難しい囲碁で、2017年に世界トップ棋士と対局して3戦全勝したのです。なぜ画期的なのか知りたい方は、ヒューバート・ドレイファス著「コンピュータには何ができないか: 哲学的人工知能批判」を読んで下さい。
さて、そのAlphaGoでは深層強化学習（deep reinforcement learning: DRL）が使われました。強化学習というのは環境から状況を観察、行動を選択し、その結果得られる報酬を最大化するという学習手法です。代表的な強化学習であるQ学習では、ある状態のときにとったある行動の価値をQテーブルと呼ばれるテーブルで管理し、行動する毎にQ値を更新していきます。このQテーブルをDNNに置換えたものがDQN（Deep Q-Network）であり、DRLはDQNを使う学習手法です。何か禅問答じみてきましたが、DL/DRLの説明はここまでとします。この後はDL/DRLをAMRのシミュレーションに導入しようと奮闘した経緯を述べます。
2. 画像DLでAMRの出発を判断（ROS1）
駄待ち狐がROSをいじりだした当初はDRLのことは何も知りませんでしたが、DLによる画像認識についてはある程度分っていました。画像DLについてはPythonの教科書でプログラミング手法も勉強しました。そこでまず、「3. 最初のROS1プログラム」でドライブする4台の中で1台がナビにこの画像DL技術を適用できないかと考えました。シミュレーション開始時の5台のTB3の位置関係から各行程の所要時間が推測できるのではないかと思い、この位置関係を画像データとして入力して所要時間の長短を判定するという学習をさせることにしたのです。この学習結果を受けて、所要時間が短い位置関係になった時に出発させようという訳です。
具体的には、world2環境を28x28のマス目に区切り、5台のTB3が居るマス目だけを白くします。さらに動きも重要だと思ったので3秒毎に5回記録して、各回ごとに初期値0のマス目に1を加算していくようにしました。これで、じっとしていれば5、通って行けば1～4、通らなければ0という6階調のグレースケール画像になります。この画像の例を以下に示しますが、左が往路で右下の真っ白のマス目がtb3_0です。tb3_0は5回の記録が終ってから出発するので、階調5になります。右の画像は復路で、右上2つの白いマス目の内の左側がtb3_0です。右側はtb3_0に進路を塞がれたTB3がその場でウロウロしている状態です。
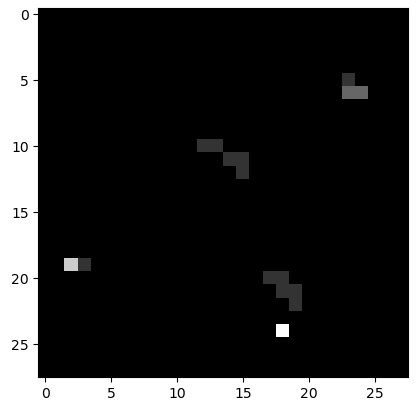
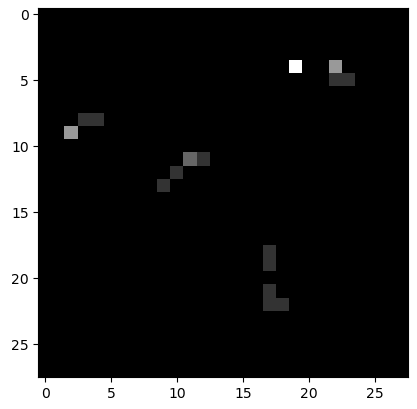
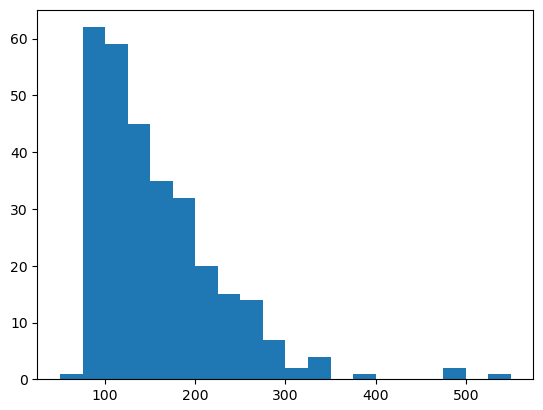
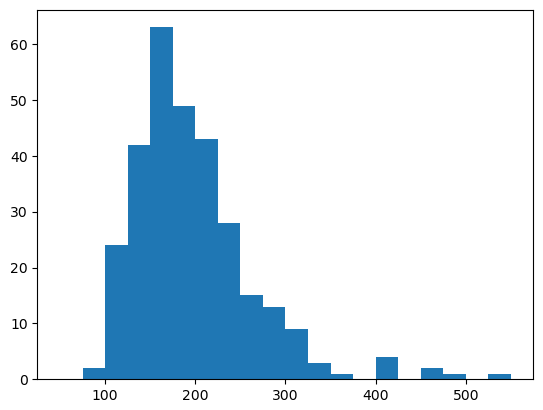
上記の初期位置画像とそれに対応する行程所要時間をセットにして、数百セット以上を蓄積したものが学習用データになります。因みに600セットを蓄積した学習用データの行程所要時間は下図のように分布しています。左のヒストグラムが往路、右が復路です。600回の合計時間は106,598秒（29.6時間）となっており、シミュレーションするのにこれだけの時間を要したということです。レッツノートでは計算速度の制約によって現実の時間がシミュレーション上の時間の3倍程度になり、これ以上早送りすることはできません。一昼夜以上シミュレーションを走らせ、夜中にも時々起きて機嫌を損ねずに動いているかどうか確認しました。
プログラムの紹介を始める前に、結論を先に述べます。5台の初期位置から行程所要時間を推測するのは不可能でした。5台のTB3は行程を重ねるごとに色々な絡み合いをするので、初期位置が決ればその行程のtb3_0の動作が決るという単純な話ではなかったのです。より正確な言い方をすれば、5台の初期位置が完全に一致していれば同じ動作をするかもしれませんが、完全に一致することはあり得ず、似た初期位置なら同じような所要時間になるという相関はないということです。画像DLの検討には158日を要しましたが、機械学習という意味では全く無駄な努力でした。ただ、その間に「4. ROS1パッケージの修正」まで完了することができました。
2.1 学習用データの記録プログラム
画像DLは①tb3_0を何回も往復させながら行程ごとの初期位置画像と所要時間を学習用データとして記録する、②学習用データを使って初期位置画像から所要時間を判定する学習を行う、③学習済みモデルに基づいて出発タイミングを決定するAI走行を行って結果を記録するという3段階になっています。この内の②はROSとは関係のないプログラムなのに対し、①と③はドライブする4台の中で1台がナビのROSプログラムにDLを付加する形になります。以下のnavi_rec_14は①と③を実行するノードで、NaviRecNodeクラスが①、AiNaviNodeクラスが③に対応します。本項では学習用データを記録するNaviRecNodeクラスについて説明します。
コードの表示にはPrism.jsを使用しています。prism.cssの設定は団塊爺ちゃんの備忘録を参考にしました。
#!/usr/bin/env python
import math
import random
import rospy
from geometry_msgs.msg import PoseStamped
from move_base_msgs.msg import MoveBaseActionResult
from nav_msgs.msg import Odometry
import message_filters
import numpy as np
import shlex
from psutil import Popen
import os
from tensorflow.keras.models import model_from_json
class NaviRecNode(object):
def __init__(self, file_name):
self.file_path = '記録用ファイルのパス' + file_name
self.fwd_flg = True # 現在の行程が行きか帰りかを示すフラッグ
self.fwd_flg_last = True # 270秒以内に到着せず再起動となった場合に再起動前の行き帰りを保存
self.spl_cnt = 0 # 1Hzのwhileループに入るとカウントアップして、秒数を計測
self.spl_cnt_last = 0 # self.spl_cntは到着後にリセットされるので、ファイル記録用に保存
self.img_data = np.zeros((1, 28, 28), dtype=float) # ロボット位置を画像で記録
self.img_data_last = np.zeros((1, 28, 28), dtype=float) # ファイル記録用に保存
self.img_last_flg = False # プログラム起動時とAI判断で出発待ちの間はファイルに記録しない
self.dpt_flg = False # AIが学習済みモデルに基づいて出発を許可しないというフラッグ
self.runs_set = rospy.get_param('runs_set') # 自動停止するまでの行程回数
rate = rospy.Rate(1)
# ゴール位置をパブリッシュするパブリッシャの宣言(ここでは宣言のみでパブリッシュはしない)
mbg_pub = rospy.Publisher(
'move_base_simple/goal', PoseStamped, queue_size=10)
# 行きと帰りで共通のゴールメッセージパラメータ
goalMsg = PoseStamped()
goalMsg.header.frame_id = 'map'
goalMsg.header.stamp = rospy.Time.now()
goalMsg.pose.position.z = 0.0
goalMsg.pose.orientation.x = 0.0
goalMsg.pose.orientation.y = 0.0
# 本ノードからm5-7.launchを起動する
# mtb3_sim内のmove_base_3.launchをm5-7.launchからコールする
self.node_process = Popen(
shlex.split('roslaunch mtb3_sim m5-7.launch')
)
# self.spl_cnt(split count)を開始するまでの時間を10～20秒でランダムに設定する
start_at = 10. + random.random()*10.
rospy.sleep(start_at)
while not rospy.is_shutdown():
'''
# 実時間270秒以内にゴールしなかったら、m5-7.launchを停止して再起動する
if self.spl_cnt > 270:
self.node_process.terminate()
rospy.sleep(15.)
self.node_process = Popen(
shlex.split('roslaunch mtb3_sim m5-7.launch')
)
# self.spl_cntをリセット後、再度開始するまでの時間を10～20秒でランダムに設定する
start_at = 10. + random.random()*10.
rospy.sleep(start_at)
self.fwd_flg_last = self.fwd_flg
self.fwd_flg = True
self.spl_cnt = 0
self.spl_cnt_last = 0
self.dpt_flg = False
'''
# move_baseのresultを受信してself.mbrCbで処理する
rospy.Subscriber(
'move_base/result', MoveBaseActionResult, self.mbrCb)
# 進行方向に合せてゴールを設定
if self.fwd_flg:
goalMsg.pose.position.x = 1.7
goalMsg.pose.position.y = -1.0
goalMsg.pose.orientation.z = -math.sqrt(2) / 2
goalMsg.pose.orientation.w = math.sqrt(2) / 2
else:
goalMsg.pose.position.x = -2.0
goalMsg.pose.position.y = -0.8
goalMsg.pose.orientation.z = 0.0
goalMsg.pose.orientation.w = 1.0
# self.spl_cnt開始後、3秒(実時間)毎にodm_subによるコールバックを行ってロボットの分布を記録
if not self.dpt_flg and (self.spl_cnt % 3 == 0):
sub0 = message_filters.Subscriber('odom', Odometry)
sub1 = message_filters.Subscriber('tb3_1/odom', Odometry)
sub2 = message_filters.Subscriber('tb3_2/odom', Odometry)
sub3 = message_filters.Subscriber('tb3_3/odom', Odometry)
sub4 = message_filters.Subscriber('tb3_4/odom', Odometry)
# message_filterを用いて複数のトピックをまとめてコールバックする
# self.subsにまとめているのはodmCb中のunregister()で使うため
self.subs = [sub0, sub1, sub2, sub3, sub4]
odm_sub = message_filters.ApproximateTimeSynchronizer(
self.subs, 10, 0.2)
odm_sub.registerCallback(self.odmCb)
# self.dpt_flgがTrueになると、分布の記録を止めて出発する
elif self.dpt_flg:
mbg_pub.publish(goalMsg)
self.spl_cnt += 1
rate.sleep()
def mbrCb(self, result):
if (result.status.status == 3) and (self.spl_cnt > 30):
self.fwd_flg_last = self.fwd_flg
self.fwd_flg = not self.fwd_flg
# self.spl_cntをリセットする前に、_lastにコピーして所要時間(実時間)をキープ
# self.fwd_flg_lastがFalseの場合、self.spl_cnt_lastに負号を付ける
self.spl_cnt_last = self.spl_cnt
if not self.fwd_flg_last:
self.spl_cnt_last *= -1
self.spl_cnt = 0
self.dpt_flg = False
def odmCb(self, odm0, odm1, odm2, odm3, odm4):
psn_data = [[odm0.pose.pose.position.x, odm0.pose.pose.position.y],
[odm1.pose.pose.position.x, odm1.pose.pose.position.y],
[odm2.pose.pose.position.x, odm2.pose.pose.position.y],
[odm3.pose.pose.position.x, odm3.pose.pose.position.y],
[odm4.pose.pose.position.x, odm4.pose.pose.position.y]]
# PythonではspinOnce()がないため、以下のunregister()でコールバックを1回だけにする
for sub in self.subs:
sub.sub.unregister()
# 5回の書込みの間、self.img_dataは0軸に沿って増える(AI判断がNGの間はローリングしていくため)
# self.img_dataの末尾image dataは初期値設定もしくは本メソッド最終行でゼロ配列とされている
img_data_size = self.img_data.shape[0]
for datum in psn_data:
m = int((2.48 - datum[0]) / 0.183)
m = min(max(m, 0), 27)
n = int((2.408 - datum[1]) / 0.172)
n = min(max(n, 0), 27)
self.img_data[img_data_size - 1, m, n] += 1
if img_data_size == 5:
# self.spl_cnt_lastが0の場合もデータをNumPy配列に記録することで、m5-7.launchの再起動を記録
# プログラム起動の初回はself.img_last_flg=Falseで、self.img_data_lastがないので記録しない
# self.spl_cnt_lastが0の場合、±1にしてfwd/bwdを識別(self.fwd_flg_lastがFalseの場合は-1)
if self.img_last_flg:
if self.spl_cnt_last == 0:
if self.fwd_flg_last:
self.spl_cnt_last = 1
else:
self.spl_cnt_last = -1
try:
data_last = np.load(self.file_path)
save_data = np.append(
data_last['arr_0'], self.img_data_last, axis=0)
cnt_data = np.append(data_last['arr_1'], self.spl_cnt_last)
# cnt_dataの要素数がself.runs_setに達するとプログラムを終了(==の時はデータを保存)
# 記録ファイルが存在しないとcnt_data[-2]が存在しないエラーになるのでtryの中でチェック
if cnt_data.size >= self.runs_set:
if cnt_data.size == self.runs_set:
np.savez(self.file_path, save_data, cnt_data)
# m5-7.launchで起動されたノードを終了する
self.node_process.terminate()
rospy.sleep(15.)
# navi_recノードを終了する
rospy.signal_shutdown(
"ALL THE TASKS HAVE BEEN ACHIEVED!")
# roscoreを終了する
os.system("killall rosmaster")
else:
np.savez(self.file_path, save_data, cnt_data)
# 出発待ちで何度も記録されるのを防ぐため、一旦self.img_last_flgをFalseにする
self.img_last_flg = False
# 記録ファイルが存在しない場合は、無条件で最初のデータを記録する
except FileNotFoundError:
save_data = self.img_data_last
cnt_data = np.array([self.spl_cnt_last])
np.savez(self.file_path, save_data, cnt_data)
# 出発待ちで何度も記録されるのを防ぐため、一旦self.img_last_flgをFalseにする
self.img_last_flg = False
# self.img_data_sumに基づいて出発の可否を判断する(記録モードでは常にTrueを返す)
self.img_data_sum = self.img_data.sum(axis=0)[None, :, :]
self.dpt_flg = self.jdgDpt()
# self.dpt_flgがTrueになると、image data_sumを_lastにコピーしてからリセット
if self.dpt_flg:
self.img_last_flg = True
self.img_data_last = self.img_data_sum
self.img_data = np.zeros((1, 28, 28), dtype=float)
# 走行モードで出発がNG場合に対応すべくself.img_data[0]を削除
img_data = np.delete(self.img_data, 0, axis=0)
# img_data_sizeが5未満の場合も含めて、self.img_dataの末尾にゼロ配列を追記
else:
img_data = self.img_data
self.img_data = np.append(
img_data, np.zeros((1, 28, 28), dtype=float), axis=0)
def jdgDpt(self):
return True
class AiNaviNode(NaviRecNode):
# 学習済みモデル(fwd)を読み込む
model_path = '学習済みモデルのパス'
try:
json_file = open(model_path + 'model_fwd.json', 'r')
loaded_model_json = json_file.read()
json_file.close
model_fwd = model_from_json(loaded_model_json)
model_fwd.load_weights(model_path + 'weight_fwd.h5')
except:
pass
# 学習済みモデル(bwd)を読み込む
try:
json_file = open(model_path + 'model_bwd.json', 'r')
loaded_model_json = json_file.read()
json_file.close
model_bwd = model_from_json(loaded_model_json)
model_bwd.load_weights(model_path + 'weight_bwd.h5')
except:
pass
def jdgDpt(self):
# self.img_data_lastをフラット化して訓練データと同じ形状にする
img_data = self.img_data_sum.reshape(-1, 784)
# img_dataを0～1に変換する
img_data = img_data / 5.
# 学習済みモデルで予測し、戻り値として0か1の予測ラベルを格納したリストを取得
if self.fwd_flg:
prd = np.argmax(self.model_fwd.predict(img_data), axis=-1)
else:
prd = np.argmax(self.model_bwd.predict(img_data), axis=-1)
# 予測ラベルが0(所定時間内で到達)なら出発し、1なら出発しない
if prd[0] == 0:
return True
else:
return False
if __name__ == '__main__':
'''
NaviRecNodeクラスは目標地点2に到達すると、5台のロボットの位置を5回記憶した後に出発し、位置と所要時間を記録
AiNaviNodeクラスはNaviRecNodeクラスを継承し、追加された学習済みモデルによる所要時間予測で出発時間を判断
AiNaviNodeクラスでは、出発と判断した時点の5回分の記憶位置と、待ち時間を含めた所要時間を記録
'''
rospy.init_node('navi_rec')
mode = rospy.get_param('mode')
if mode == 'rec':
nr = NaviRecNode('learn_data.npz') # 引数は学習用データを記録するファイル名
else:
an = AiNaviNode('ai_results.npz') # 引数はAI走行結果を記録するファイル名
# プログラムの正常停止はodmCb関数のtry文の中で条件判断によって行われるので、ここには停止処理がない
NaviRecNodeクラスの元になっているのは目標姿勢を設定するノード（最終版はmtb3_navi_2）で、31～40行目と71～84行目はmtb3_navi_2のままです。これ以外の追加部分ですが、まず42～46行目はローンチファイルの建付けを変えたことに関係しています。mtb3_navi_2は全てのノードを起動するnavi_drive3.launchによって実行されますが、navi_rec_14はこのノードのみを起動するnavi_rec.launchによって実行され、navi_rec_14の中で自分以外の残りのノードを起動するm5-7.launchを実行します。なぜこんなややこしいことにしたかというと、tb3_0が動けなくなった時にシミュレーションを最初からやり直すことにしていたからです。
そのやり直しが53～69行目ですが、ご覧の通りコメントアウトされています。ROS1パッケージの修正によってtb3_0が動けなくなることはなくなったので、シミュレーションを最初からやり直す必要もなくなったのです。従って「こんなややこしいこと」も不要なのですが、プログラム開発の経緯を受けてnavi_rec_14にはこの建付けが残っています。47～49行目も実は不要だったのですが、毎回同じシミュレーションを繰返すことになるのではないかという懸念から出発時間をランダムに遅延させるということをやっていました。実際にはそんなことをしなくても、ドライブとナビは千差万別の動きをします。
86～99行目が初期位置を記録する部分です。tb3_0～４の位置情報をodomトピックで取得してodmCb関数をコールバックします。odmCb関数の131～139行目で位置座標を28x28のマス目に変換し、shapeが(1, 28, 28)の3次元NumPy配列self.img_dataの対応する要素に1を加算します。コメントにある通り、この段階では5回分を足してしまわずにaxis=0に沿って重ねていきます。これはNaviRecNodeクラスを継承するAiNaviNodeクラスで5回分の足し算をローリングしていく必要があるためです。185行目でaxis=0に沿った足し算を行ってself.img_data_sumとしており、これが各行程ごとの画像データとなります。
各行程の画像データをaxis=0に沿って重ねたデータはtrain_data.npzというファイル名で保存されます。このファイル名は255行目でNaviRecNodeインスタンスを生成する際の引数として指定され、19行目でself.file_pathに引継がれます。npzファイルは複数のNumPy配列を保存するバイナリファイルで、train_data.npzのarr_0が初期位置画像、arr_1が所要時間となっています。先程のself.img_data_sumは191行目でself.img_data_lastとして保持し、153～155行目で前回保存したtrain_data.npzのarr_0にappendしてsave_dataとします。save_dataは172行目でtrain_data.npzに上書き保存されます。
所要時間については、105～106行目で1秒ごとにカウントアップされるself.spl_cntを114行目でself.spl_cnt_lastとして保持しています。従って、この所要時間はシミュレーション時間ではなくその3倍の実時間で、初期位置画像を記録する時間も含んでいます。往路と復路の所要時間を識別するために、115～116行目で復路の場合はself.spl_cnt_lastに負号を付けます。156行目で前回保存したtrain_data.npzのarr_1にself.spl_cnt_lastをappendしてcnt_dataとします。cnt_dataの要素数がself.runs_setに達すると158～170行目でプログラムを終了します。
2.2 所要時間判定の学習プログラム
初期位置画像と所要時間を関連付けるには、往路と復路を分けた方がいいだろうと考えました。また、学習用データとしては訓練データとテストデータが必要です。以下のPythonプログラムでは、7～8行目でsave_dataとcnt_dataの中の往路のみを残してsave_data_fwdとcnt_data_fwdにしています。10～13行目ではsave_data_fwdをx、cnt_data_fwdをyとして、それぞれの_trainと_testを作成します。15行目でx_train、y_train、x_test、y_testをtrain-test_fwd.npzに保存すれば、学習プログラムに必要な往路の学習用データが出来上ります。復路についても同様なので、この後も往路についてのみ説明していきます。
import numpy as np
data = np.load('(記録用ファイルのパス)/learn_data.npz')
save_data = data['arr_0']
cnt_data = data['arr_1']
# cnt_dataが正のデータのみを残す
save_data_fwd = np.delete(save_data, np.where(cnt_data < 0), axis=0)
cnt_data_fwd = np.delete(cnt_data, np.where(cnt_data < 0))
# fwdデータを訓練データとテストデータに分割
x_train = np.delete(save_data_fwd, slice(200, 300), axis=0)
y_train = np.delete(cnt_data_fwd, slice(200, 300))
x_test = np.delete(save_data_fwd, slice(0, 200), axis=0)
y_test = np.delete(cnt_data_fwd, slice(0, 200))
# NumPy配列をnpzファイルに保存
np.savez('(記録用ファイルのパス)/train-test_fwd.npz', x_train, y_train, x_test, y_test)
初期位置画像から所要時間を判定する学習プログラムは以下の通りですが、Pythonの教科書に載っていたプログラムをほとんどそのまま転用しています。教科書のプログラム自体もグーグルが提供するKerasライブラリの演習例題のようなもので、0から9までの手書き数字のモノクロ画像（28x28ピクセル、256階調）を使って学習します。KerasはTensorFlowライブラリを簡単に使えるようにするラッパーライブラリで、手書き数字画像はライブラリの中に訓練用として6万枚、テスト用に1万枚が収録されています。それに比べると駄待ち狐の200枚、100枚というのはシケた枚数ですが、30時間かかってこれだけなので致し方ありません。
import numpy as np
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
from tensorflow.keras.optimizers import Adam
npz_data = np.load('(記録用ファイルのパス)/train-test_fwd.npz')
x_train = npz_data['arr_0']
y_train = npz_data['arr_1']
x_test = npz_data['arr_2']
y_test = npz_data['arr_3']
# xデータをフラット化する
x_train = x_train.reshape(-1, 784)
x_test = x_test.reshape(-1, 784)
# xデータを0～1に変換する
x_train = x_train / 5.
x_test = x_test / 5.
'''
# yデータを5段階に分け、ワンスポット表現に変換
y_train1 = np.where(y_train < 100, 0, y_train)
y_train2 = np.where((y_train1 >= 100) & (y_train1 < 150), 1, y_train1)
y_train3 = np.where((y_train2 >= 150) & (y_train2 < 200), 2, y_train2)
y_train4 = np.where((y_train3 >= 200) & (y_train3 < 250), 3, y_train3)
y_train = np.where((y_train4 >= 250), 4, y_train4)
y_test1 = np.where(y_test < 100, 0, y_test)
y_test2 = np.where((y_test1 >= 100) & (y_test1 < 150), 1, y_test1)
y_test3 = np.where((y_test2 >= 150) & (y_test2 < 200), 2, y_test2)
y_test4 = np.where((y_test3 >= 200) & (y_test3 < 250), 3, y_test3)
y_test = np.where((y_test4 >= 250), 4, y_test4)
num_classes = 5
'''
# 出力を2段階に分け、ワンスポット表現に変換
data_th = 150
y_train1 = np.where(y_train < data_th, 0, y_train)
y_train = np.where(y_train1 >= data_th, 1, y_train1)
y_test1 = np.where(y_test < data_th, 0, y_test)
y_test = np.where(y_test1 >= data_th, 1, y_test1)
num_classes = 2
y_train = to_categorical(y_train, num_classes)
y_test = to_categorical(y_test, num_classes)
# ニューラルネットワークの作成
model = Sequential()
# 第1層の作成
model.add(Dense(512,
input_shape=(784,),
activation='relu'))
# ドロップアウトの実装
model.add(Dropout(0.20))
# 第2層（出力層）の作成
model.add(Dense(num_classes,
activation='softmax'
))
# バックプロパゲーションの実装
model.compile(
loss='categorical_crossentropy',
optimizer=Adam(),
metrics=['accuracy'])
# ニューラルネットワークの構造を出力
model.summary()
# ディープラーニングの実行
batch = 32
epochs = 10
history = model.fit(x_train,
y_train,
batch_size=batch,
epochs=epochs,
verbose=1,
validation_data=(
x_test, y_test
)
)
# 学習結果の評価
score = model.evaluate(x_test, y_test, verbose=0)
print('test loss: ', score[0])
print('test accuracy: ', score[1])
# 学習結果の保存
with open('(学習済みモデルのパス)/model_fwd.json', 'w') as json_file:
json_file.write(model.to_json())
model.save_weights('(学習済みモデルのパス)/weight_fwd.h5')
教科書のプログラムから唯一変更している箇所は、y_train、y_testの要素を変換する部分です。元の要素は所要時間そのものですが、これをn段階に区切って0～(n-1)に置換えています。最初はコメントアウトしてある20～31行目のように5段階にしていたのですが、「③学習済みモデルに基づいて出発タイミングを決定する」のに使うのであれば出発するかしないかの2段階で十分だと思い直し、34～40行目のようにしました。このプログラムを実行した結果は以下の通りで、最終行のtest accuracy:は 0.51という情けない数字です。2択ですからデタラメを言っても5割は当ります。0.51というのは何も予測できていないということです。
%runfile /home/kenichi/catkin_ws/ai_navi/Learn_fwd.py --wdir
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_6 (Dense) (None, 512) 401920
dropout_3 (Dropout) (None, 512) 0
dense_7 (Dense) (None, 2) 1026
=================================================================
Total params: 402,946
Trainable params: 402,946
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
7/7 [==============================] - 0s 17ms/step - loss: 0.6904 - accuracy: 0.5300 - val_loss: 0.6895 - val_accuracy: 0.5700
Epoch 2/10
7/7 [==============================] - 0s 6ms/step - loss: 0.6461 - accuracy: 0.6250 - val_loss: 0.6923 - val_accuracy: 0.5500
Epoch 3/10
7/7 [==============================] - 0s 5ms/step - loss: 0.6150 - accuracy: 0.7950 - val_loss: 0.6965 - val_accuracy: 0.5100
Epoch 4/10
7/7 [==============================] - 0s 5ms/step - loss: 0.5731 - accuracy: 0.9200 - val_loss: 0.6997 - val_accuracy: 0.5300
Epoch 5/10
7/7 [==============================] - 0s 6ms/step - loss: 0.5412 - accuracy: 0.9250 - val_loss: 0.7049 - val_accuracy: 0.5400
Epoch 6/10
7/7 [==============================] - 0s 7ms/step - loss: 0.4946 - accuracy: 0.9100 - val_loss: 0.7164 - val_accuracy: 0.5400
Epoch 7/10
7/7 [==============================] - 0s 6ms/step - loss: 0.4510 - accuracy: 0.9400 - val_loss: 0.7293 - val_accuracy: 0.5100
Epoch 8/10
7/7 [==============================] - 0s 5ms/step - loss: 0.4148 - accuracy: 0.9450 - val_loss: 0.7459 - val_accuracy: 0.5100
Epoch 9/10
7/7 [==============================] - 0s 5ms/step - loss: 0.3668 - accuracy: 0.9600 - val_loss: 0.7648 - val_accuracy: 0.4900
Epoch 10/10
7/7 [==============================] - 0s 6ms/step - loss: 0.3284 - accuracy: 0.9600 - val_loss: 0.7961 - val_accuracy: 0.5100
test loss: 0.7961411476135254
test accuracy: 0.5099999904632568
2.3 学習に基づく走行プログラム
何も予測できない学習結果に基づいてAI走行を行っても意味はありませんが、プログラムとして完成させるために前述のnavi_rec_14にはAI走行用のAiNaviNodeクラスがあります。NaviRecNode自体もこれに対応して補完されています。AiNaviNodeでは学習済みモデルを読込む207～225行目が追加され、オーバーライドされたjdgDpt()関数が所要時間を予測します。判定結果が「長い」であれば待機し、「短い」であれば出発するという部分はNaviRecNodeの101～103行目にあり、このself.dpt_flgはodmCb()関数の186行目でjdgDpt()関数を実行して取得します。NaviRecNode自身のjdgDpt()関数は203行目にある通り常にTrueを返します。
NaviRecNodeを実行した時はjdgDpt()関数が常にTrueを返すので、初期位置画像を5回取得したらすぐに出発です。一方、AiNaviNodeを実行すると、その5回分の初期画像に基づいて判定した所要時間が「短い」であればすぐに出発しますが、「長い」であれば待機します。待機中も3秒毎に5台のTB3の位置を記録しますが、初期画像は5回分の重ね合せなのでローリングしながら足し算する必要があります。このためodmCb()関数の195行目でself.img_data[0]を削除しています。常に最新の5回分を足し算した初期画像を使って所要時間を予測する訳です。
前項までの説明に用いてきた600回走行データは「4. ROS1パッケージの修正」まで行った後に蓄積したものですが、この学習済みモデルについてはAI走行を行っていません。その2年前に「3. 最初のROS1プログラム」の段階でも1,000回の走行データを蓄積し、やはり何も予測できないという結果になり、それでもAI走行を行って何の効果もないことを確認していたからです。この確認内容が以下のヒストグラムです。左はAIなしで100回の走行を行った時の所要時間、右はAI走行を行った時の所要時間を橙色で重ね書きしています。デタラメを言うAIに従って出発を待った分だけ余計に時間がかかっています。
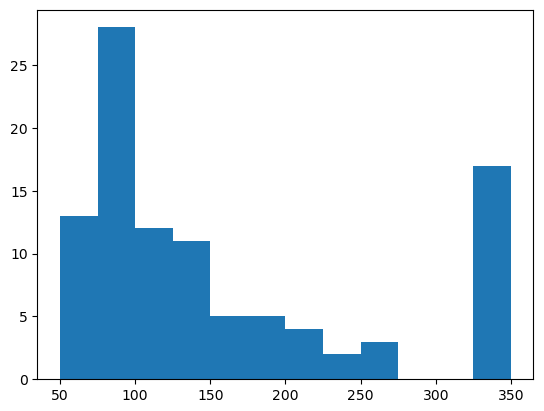
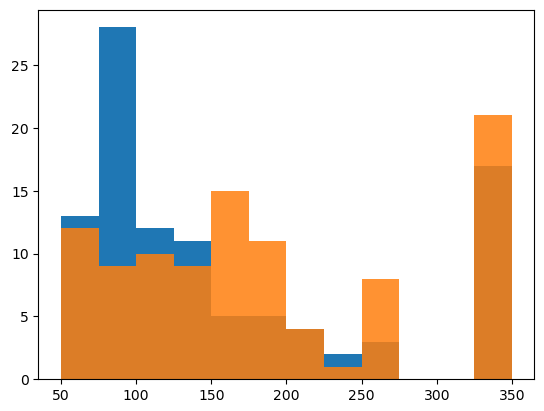
因みにヒストグラムで325～350秒のところにカウントされているのは、tb3_0が動けなくなってシミュレーションを最初からやり直した回数です。実際のプログラムでは270秒でゴールできなければnavi_rec_14が自分以外のノードを再起動します。100回の走行で17回ないしは21回の再起動が発生しており、頻繁に動けなくなっていました。それが「4. ROS1パッケージの修正」まで行った後に行った600回の走行では1回も再起動は発生していません。というか、再起動プログラムそのものをコメントアウトしています。機械学習はうまく行かなかったものの「4. ROS1パッケージの修正」まで完了した成果はここに現れています。
3. DRLでエレベータの出発を判断（AnyLogic）
「VIII. AMRのモデリングシミュレーション」の「4. エレベータによるフロア間移送」で書いた通り、駄待ち狐がAnyLogicで最初に作ったモデルは作業員がかご台車をエレベータで運ぶというものでした。そのモデルでは作業員がかご台車を押して透明人間のすれ違いをしていましたが、この時点（2021年11月）でAnyLogicに機械学習を導入できないかと考えました。グーグってみると、AnyLogic社のサイトで"Artificial Intelligence and Simulation in Business"という白書が公開されていました。AnyLogicにAIを取込むならDRLだということのようです。DRLはDNNを使うという点は画像DLと共通ですが、学習のための環境モデルが必要になります。
画像DLがKerasで簡単に実装できたように、DRLはKeras-RLライブラリで実装できます。ところがKeras-RLはPythonなので、Javaしか扱えないAnyLogicでは使うことができません。とはいえ蛇の道は蛇、JavaでDRLを行うためのRL4J（reinforcement learning for Java）というライブラリがありました。①そもそもDRLについてよく分っていない、②RL4Jに関する情報はKeras-RLに比べて圧倒的に少ない、③RL4JをAnyLogicに適用した実例は"Traffic Light Example"（信号機）しか見つからずソースコードは一部しか公開されていないという三重苦の中で、Javaアプレット以来四半世紀ぶりのJavaとの格闘です。
「信号機」はThe AnyLogic Conference 2019, Austin, TXで発表された"Practical Applications of Deep Reinforcement Learning Using AnyLogic"という講演に出てきます。2021年にグーグった時はこの講演のスライドPDFがダウンロードできたのですが、今（2025年4月15日）グーグっても講演の動画しか出てきません。公開されていない人様のPDFを勝手に紹介する訳にはいきませんが、信号機の赤と青をどのようなタイミングで切替えれば交差点の待ち時間を最短にできるかというシミュレーションです。ソースコード全体は公開されておらず、PDFにはRL4JをAnnyLogicで使う際にポイントとなるコードだけが掲載されています。
3.1 Python（Keras-RL）の練習問題
①に関してはまず深層強化学習に関する記事をグーグって、ちゃんと説明されているものを精読しました。その後はプログラム例を探しますが、一番分りやすかったのが「Keras-RLで簡単に強化学習(DQN)を試す」です。直線上を動く点が-1～+1の範囲のランダムな初期位置から出発し、加速度を操作して原点で静止する（位置と速度の絶対値が0.1未満になる）ように学習します。課題としてはシンプルで、DRLを使うまでもなく数式でプログラミングできそうですが、DRLの学習過程を分りやすくビジュアル化できます。元のプログラムは学習後のテスト結果をグラフ表示するだけですが、学習の最初から10回ごとの結果を表示するようにしました。
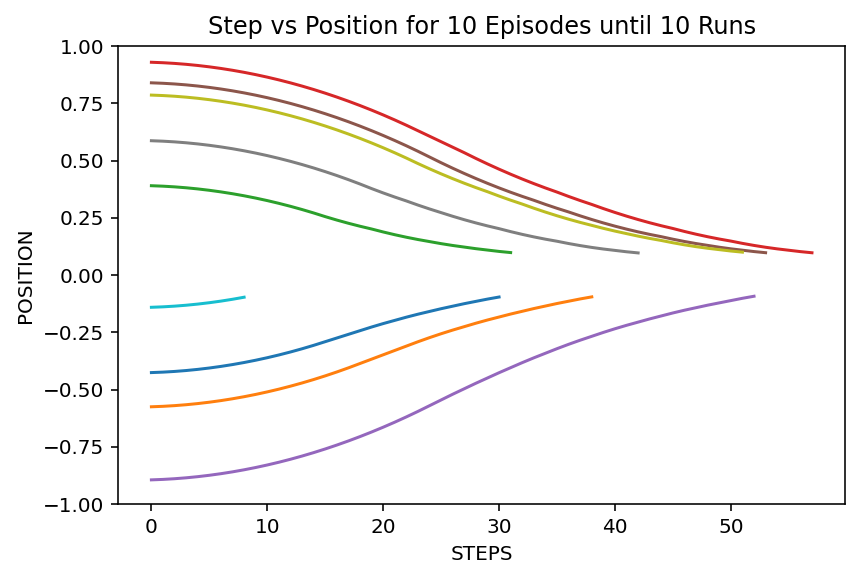
上図はテスト結果ですが、画像をクリックすると学習の過程が表示されます。「10回ごとなのに9本しかないよ」と言われそうですが、初期位置が-0.1～+0.1の範囲だといきなり上がりで曲線は表示されません。プログラムは以下の2つに分れており、main.pyではDQNのネットワーク定義をして訓練とテストを実行します。実際にはkerasとrl（keras-rl）から色々なモジュールをインポートしてパラメータを設定しています。もう一つのmoveEnv.pyには環境設定クラスPointOnLine()が記述されています。PointOnLine()はgym.core.Envを継承していますが、gymはDRLのシミュレーションライブラリです。
from keras.models import Sequential
from keras.layers import Dense, Activation, Flatten
from keras.optimizers import Adam
from rl.agents.dqn import DQNAgent
from rl.policy import EpsGreedyQPolicy
from rl.memory import SequentialMemory
import moveEnv
# 環境設定クラスPointOnLineのインスタンスを生成
env = moveEnv.PointOnLine()
# アクション空間内のactionの数をn_actionに代入
n_action = env.action_space.n
# DQNのネットワーク定義
model = Sequential()
model.add(Flatten(input_shape=(1,) + env.observation_space.shape))
model.add(Dense(16))
model.add(Activation('relu'))
model.add(Dense(16))
model.add(Activation('relu'))
model.add(Dense(16))
model.add(Activation('relu'))
model.add(Dense(n_action))
model.add(Activation('linear'))
print(model.summary())
# モデルのコンパイル
# experience replay用のmemory
memory = SequentialMemory(limit=50000, window_length=1)
# 行動方策はオーソドックスなepsilon-greedy
# 他に、各行動のQ値によって確率を決定するBoltzmannQPolicyが利用可能
policy = EpsGreedyQPolicy(eps=0.1)
dqn = DQNAgent(
model=model, nb_actions=n_action, memory=memory, nb_steps_warmup=100,
target_model_update=1e-2, policy=policy)
dqn.compile(Adam(lr=1e-3), metrics=['mae'])
# 訓練
dqn.fit(
env, nb_steps=20000, visualize=False, verbose=2, nb_max_episode_steps=300)
# テスト
env.reset(1)
dqn.test(env, nb_episodes=10, visualize=False)
env.reset(2)
import gym
import gym.spaces
import numpy as np
import matplotlib.pyplot as plt
# 直線上を動く点の速度を操作し、目標(原点)に移動させることを目標とする環境
class PointOnLine(gym.core.Env):
def __init__(self):
self.stepCnt = 0 # 300ステップでゴールしなかった時に停止させるカウンタ
self.episCnt = 0 # エピソード10回毎にグラフを表示するためのカウンタ
self.posLog = [] # 全ステップにおけるposをエピソード毎に記録するリスト
self.figNum = 0 # グラフを出力するファイルの名前に付ける通し番号
# 速度を下げる、そのまま、上げるの3種のactionを含む行動空間を規定
self.action_space = gym.spaces.Discrete(3)
# 観測空間の次元(位置と速度の2次元)とそれらの最大値をNumPy配列で規定
high = np.array([1.0, 1.0])
# 最小値は最大値の符号反転として、観測空間を規定
self.observation_space = gym.spaces.Box(low=-high, high=high)
# 各ステップごとに呼ばれるメソッド
# actionを受け取り、次のstateとreward、エピソードが終了したかどうかを返す
def step(self, action):
dt = 0.1 # Δtのこと
# 3種のaction(0, 1, 2)を加速度(acc)に変換
acc = (action - 1) * 0.1
self._vel += acc * dt
# 速度の最小値を-1.0、最大値を1.0に設定する
self._vel = max(-1.0, min(self._vel, 1.0))
self._pos += self._vel * dt
# 位置の最小値を-1.0、最大値を1.0に設定する
self._pos = max(-1.0, min(self._pos, 1.0))
# posLogリストにposを追記
self.posLog.append(self._pos)
# 位置と速度の絶対値が0.1より小さくなったらエピソードを終了
done = abs(self._pos) < 0.1 and abs(self._vel) < 0.1
# 終了したときに正の報酬
if done:
reward = 1.0
# 時間経過ごとに負の報酬
# ゴールへの距離が近くなるほど絶対値を減らしておくと、学習が早く進む
else:
reward = -0.01 * abs(self._pos)
# ステップ数が300回を超えるとエピソードを終了
self.stepCnt += 1
if self.stepCnt > 300:
done = True
# 次のstate、reward、終了したかどうか、追加情報を順番に返す
# 追加情報は特にないので空dictとする
return np.array([self._pos, self._vel]), reward, done, {}
# 各エピソードの開始時に呼ばれ、初期stateをNumPy配列で返す
def reset(self, modeNum=0):
# 初期位置は-1.0～1.0のランダム、速度は0.0
self._pos = np.random.rand()*2 - 1
self._vel = 0.0
# テスト開始時にmodeNum=1でreset()が呼ばれた時の処理
if modeNum == 1:
self.episCnt = -1
plt.clf()
# エピソード10回分のグラフを重ねて表示
else:
plt.plot(self.posLog)
if self.episCnt % 10 == 0 and self.episCnt != 0:
plt.ylim(-1., 1.);
plt.title(
"Step vs Position for 10 Episodes until "
+ str(self.episCnt) + " Runs")
plt.xlabel("STEPS")
plt.ylabel("POSITION")
plt.savefig("(グラフ保存フォルダのパス)/F" + str(self.figNum) + ".png")
self.figNum += 1
plt.pause(0.1)
# 訓練時の描画は更新のためクリアするがテスト時の描画はクリアしない
if modeNum != 2:
plt.clf()
# stepカウンタをリセット
self.stepCnt = 0
# episodeカウンタを加算
self.episCnt += 1
# posLogリストをクリア
self.posLog = []
return np.array([self._pos, self._vel])
DRLは環境から状況を観察、行動を選択してその結果得られる報酬を最大化しますが、行動選択→状況観察→報酬決定のサイクルをステップと呼び、連続するステップが一区切りする（本例では点がゴールする）までをエピソードと言います。各ステップごとに呼ばれるstep()メソッドは引数がactionで、state、reward、done（エピソード終了）を返します。この例ではaction（0～2の3値から選択)を加速度に変換し、速度と位置を計算してstateにします。ゴールすればdoneをTrueにして、1.0のrewardを与えます。ゴールした時しか報酬を出さないとなかなか学習しないので、ゴール時以外は原点からの距離に応じた負のrewardとします。
reset()メソッドは各エピソードの開始時に呼ばれて初期stateを返しますが、本例では54～55行目で初期stateを設定し、77行目でstepカウンタをリセットしている以外は、グラフの表示と保存のためのコードです。引数modeNumもテスト結果をグラフ表示する際の小技で、main.pyの39行目と41行目でmodeNumを1と2にしてreset()を呼んでいます。本項冒頭に示したスライドショーは保存したグラフをJavaScriptで表示していますが、IDE（統合開発環境）にAnacondaのSpyderを使えば、プログラム実行時にプロットペインにグラフが順次表示されます。但し計算に時間がかかるので、スライドショーのように1秒おきに表示という訳にはいきません。
3.2 Java（RL4J）に練習問題を移植
②に進むにはJavaのIDEが必要です。1997年にはMRJSDKを使いましたが、現在の定番はEclipseのようです。最終的にAnyLogicに移植する際には依存ライブラリを集約したuberjarファイルが必要になるので、uberjarを生成することができるMavenもインストールします。MavenはJavaのビルド自動化ツールです。Eclipseのプロジェクト（プログラムの管理単位）としてはJavaプロジェクトではなくMavenプロジェクトを使います。EclipseにもMavenにもWindows版とUbuntu版がありますが、AnyLogicにWindows版を使っているのであればそれに合せます。
いきなりRL4Jのプログラムは書けないので、まずはサンプルコード探しです。色々グーグった結果、deeplearning4j-examplesパッケージをgit cloneした中にあるrl4j-examplesフォルダがそのままMavenプロジェクトになっていることが分りました。rl4j-examplesをEclipseにインポートして、src/main/java/org/deeplearning4j/rl4j/examples/advanced/cartpoleという奥深いところにあるソースコードDQNCartpole.javaを唯一の頼りとしました。また穴があくほどこのプログラムを眺め、「信号機」のPDFも参考にしながら上述のPython練習問題をJavaに移植しました。
ところがなぜか現時点（2025年4月）では、deeplearning4j-examplesをダウンロードしてもrl4j-examplesが入っていません。消えてしまった理由は分りませんが、駄待ち狐が移植した練習問題を紹介すれば事足りると思います。ソースコードはZIPで丸ごとダウンロードできます。解凍後のdrl_testフォルダを既存MavenプロジェクトとしてEclipseにインポートすると、src/main/javaフォルダの中にMoveToOrigin.javaとMoveMDP.javaという2つのファイルが入っています。前者がPythonのmain.py、後者がmoveEnv.pyに相当します。やっていることは同じなのですが、コードの書きぶりは全然別世界です。
さて、このMoveToOrigin.javaを実行しても、暫く（数分～数十分）は全く動きません。何をしているかというと、依存ライブラリを自動的にダウンロードしているのです。PythonのSpyderであれば「依存ライブラリがありません！」と怒られて、conda installなりpip installなりする訳ですが、Eclipseは黙々と依存ライブラリをダウンロードしてくれます。この時の水先案内人がプロジェクト・エクスプローラーの一番下にあるpom.xmlで、この仕組みを提供しているのがMavenなのです。これはこれで素晴しい仕組みだと思うのですが、プログラムを実行したのにエラーもインフォも吐かずにただ黙っているので、ハングアップしたのかと思いました。
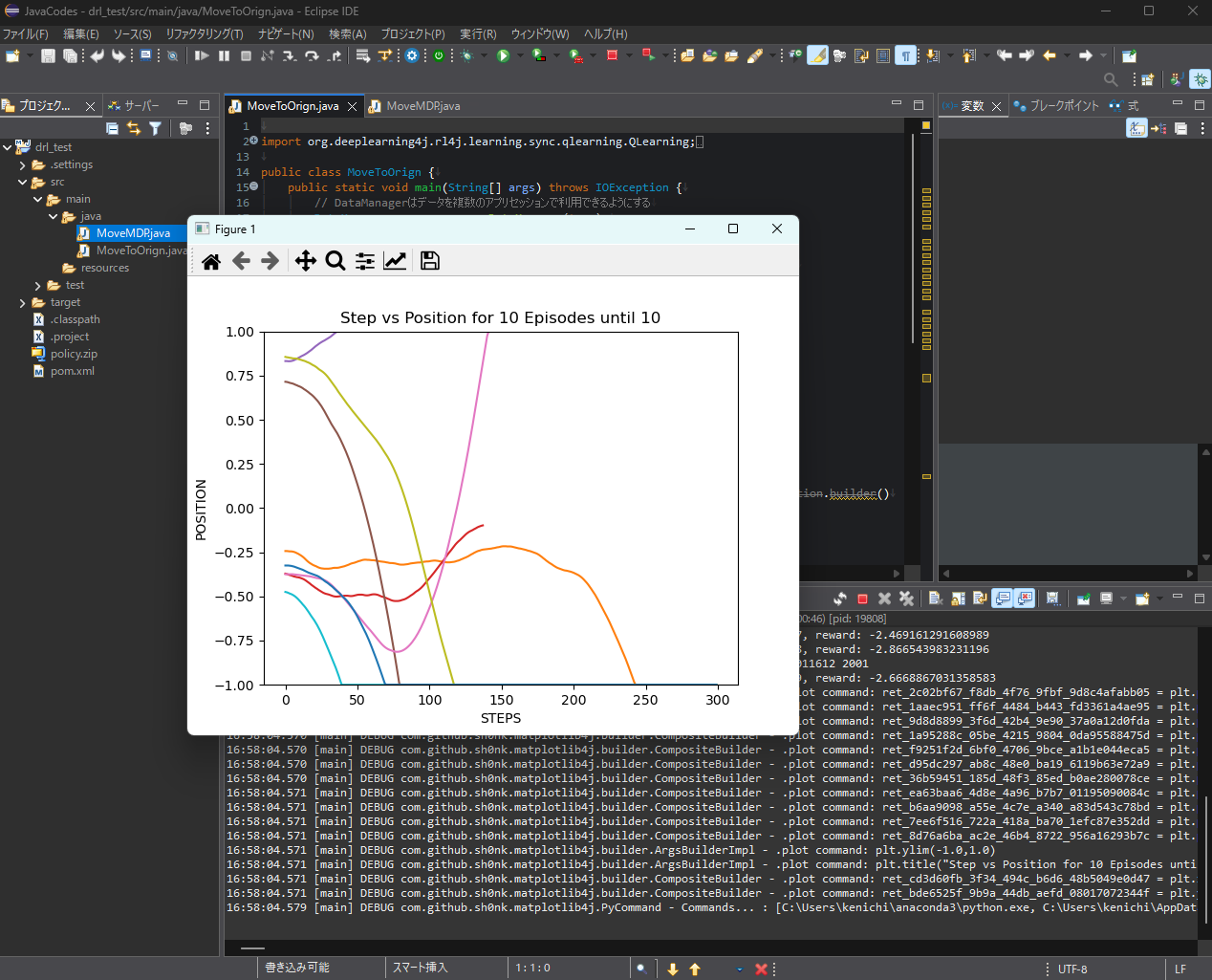画像を新しいタブで開くと高解像度で見ることができます。
ようやくプログラムが走り出すと、今度は上記の状態で止ります。Figure 1ウィンドウを手動で閉じてやれば実行を再開しますが、最後にテスト結果を表示するまで何十回もFigureウィンドウを閉じる必要があります。なぜこんな面倒なことになっているかというと、PythonのMatplotlibライブラリをJavaに移植したMatplotlib4jでは、プログラムを止めずにグラフをプロットするという動作が実現できなかったためです。何にせよ、最後までプログラムを走らせればPythonと同じような学習経過とテスト結果が得られます。これでJavaのRL4Jを使ってDRLを実行するところまでこぎつけました。